I'm an Artificial Life researcher. WTF is Artificial Life? I also run a hacker house for researchers: calculus.house
There's no particular problem I'm trying to solve, but what I'm really interested in is developing an intuitive understanding of how and why life happens.
Some of the questions I'll need to answer to get there:
- What is complexity? How does it emerge?
- What is information? How do you describe life as an informational process?
- What is computation? How and why does matter compute?
I believe creating artificial life is a good test for whether you understand life, but an even better test is designing life. This is analogous to both creating AGI and solving the alignment problem. I'm also certain that computer simulations are by far the most effective tool for studying artificial life. More on my research philosophy.
I'm also an AI power user, and I publish my entire conversation history here.
Research
Dynamical systems for generalists
[Blog]
Dynamical systems theory is a field which has largely been abandoned since the 1990s when chaos was still a hot topic. It was developed by mathematicians studying general forms of differential equations and the kinds of behaviors they can exhibit. That's why the theory is incredibly difficult to learn. The best resources are buried in pages of proofs about abstract function spaces and ergodic measures, so it's nearly impossible for physicists, biologists and ML researchers to make sense of it. At this point I've exhausted every available resource on dynamical systems and I have yet to find one which would make sense to a non-mathematician. That's why I wrote this post!
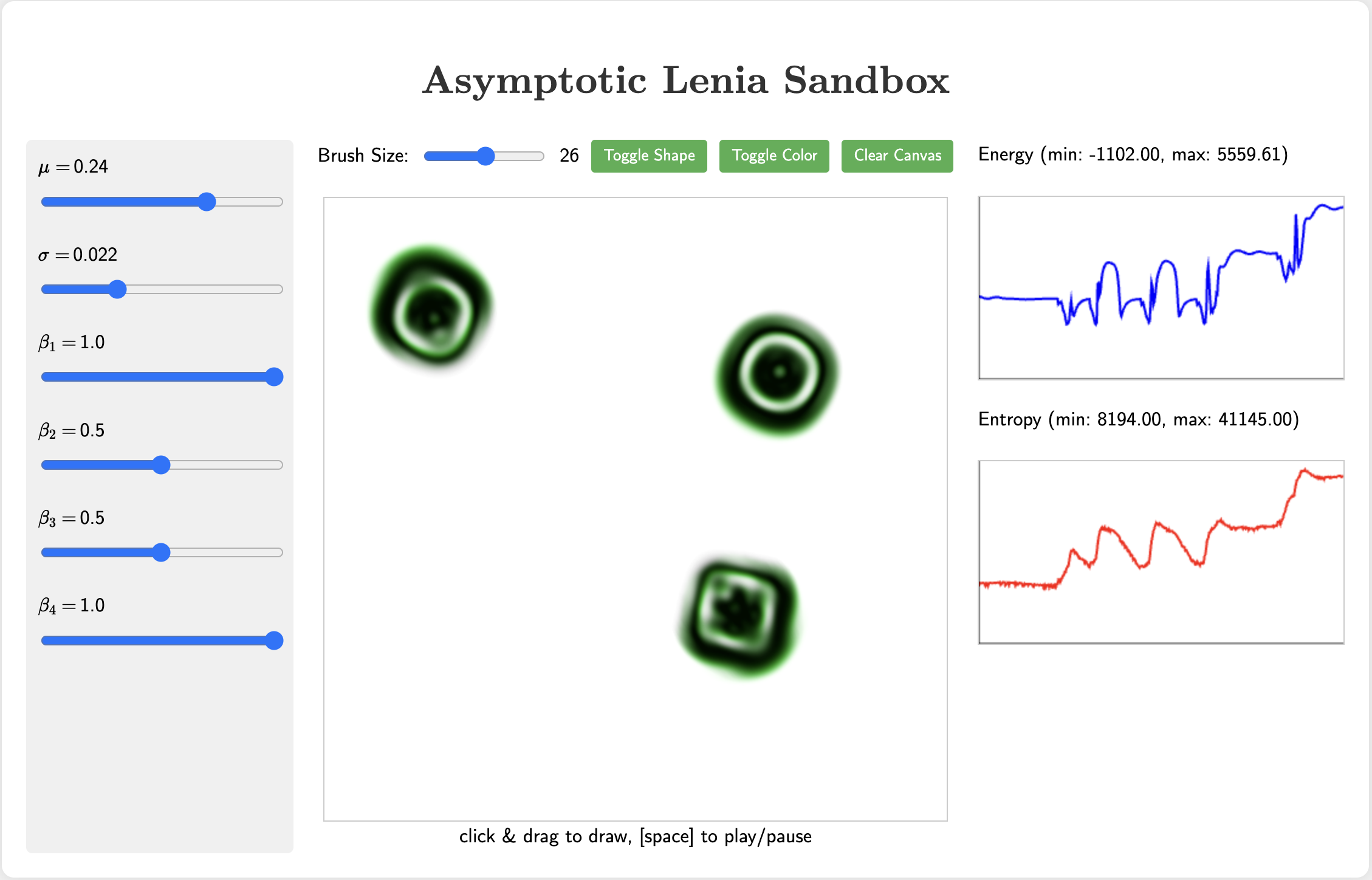
Asymptotic Lenia playground
Hey! You might be wondering what's going on here. Lenia is a continuous version of Conway's Game of Life, meaning the cells take on a values between 0 and 1 and space and time are defined on an infinitely small grid. Just like GoL, each cell looks at its neighbors and decides whether to increase or decrease using a function called the growth function. To make the math nice, we model this with a partial differential equation for the state of the system \(A(\mathbf{x}, t)\):
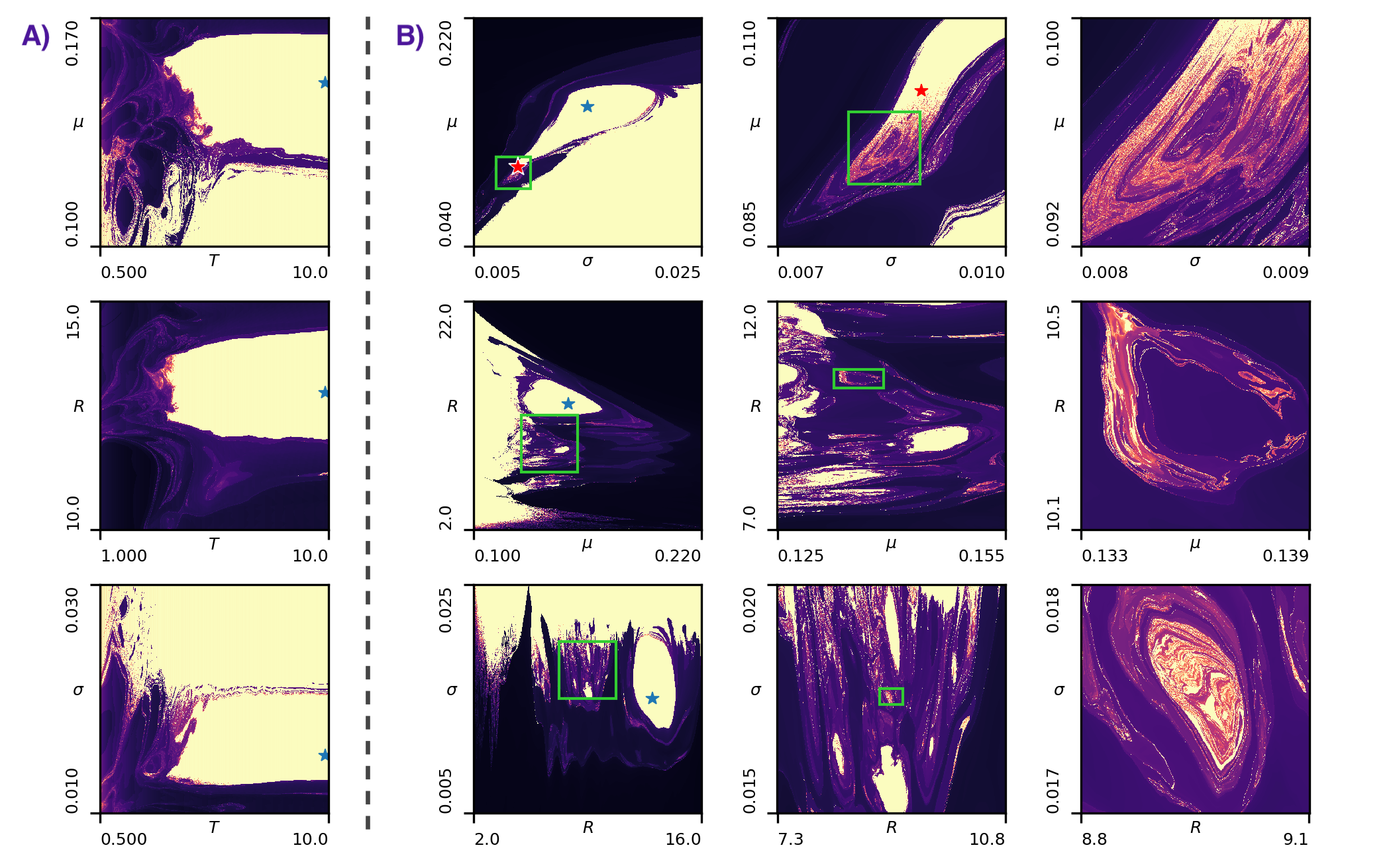
Classifying the fractal parameter space of the Lenia Orbium
The Lenia family of continuous cellular automata can be viewed as the iterative application of a constant function with unpredictable convergence properties. This makes it mathematically analogous to the Mandelbrot set and neural network trainability, which have both been shown to have fractal convergence boundaries. Using an escape-time algorithm, we plot the stability of the Orbium unicaudatus species as a function of two parameters at a time, generating fractals that persist on multiple spatial scales. We categorize regions in this parameter space and explore them to find a set of familiar species, one novel specimen, and many non-trivial variations of Orbium that fundamentally rely on discretization to survive. Based on these discoveries, we hypothesize the existence of many complex undiscovered species hidden in the fractal parameter spaces of the rest of the Lenia zoo.